

If $$x$$ is approaching one of the transition points of the function, then you have to check both one-sided limits.
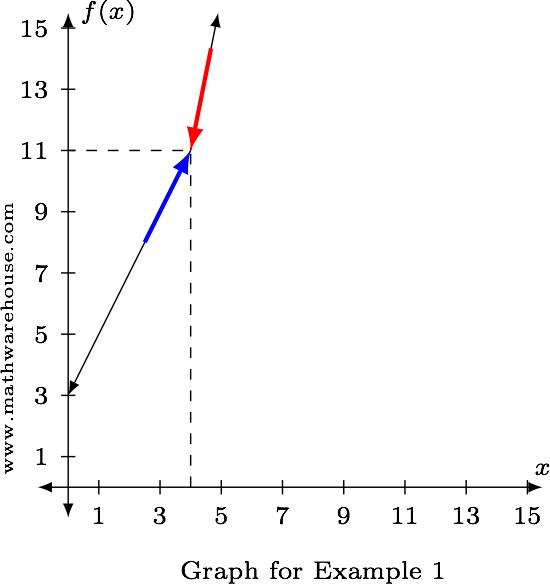
Determine $$\displaystyle\lim\limits_ f(x)$$, if $$f$$ is defined as below.
Evaluate the one-sided limits.
If the one-sided limits are the same, the limit exists.
Answer: $$\displaystyle\lim\limits_f(x) = 11$$ when $$f$$ is defined as above.
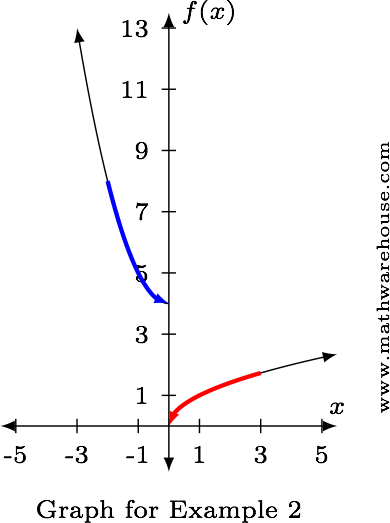
Evaluate $$\displaystyle\lim\limits_ f(x)$$ when $$f$$ is defined as follows.
If the one-sided limits are different, the limit doesn't exist.
Answer: $$\displaystyle\lim\limits_ f(x)$$ doesn't exist when $$f$$ is defined as above.
Suppose $$f$$ is defined as below. Determine the value of $$b$$ so that $$\displaystyle\lim\limits_ f(x)$$ exists.
$$ \begin% \lim_ f(x) & = \lim_(2x-3) = 2(5)-3 = 7\\ \\ \lim_ f(x) & = \lim_\left(\frac 2 3 x + b\right) = \frac 3 + b = \frac 3 + b \end $$
Set the two limits equal to each other and solve.
$$ \\ \begin \frac 3 + b & = 7\\[6pt] b & = 7 - \frac 3\\[6pt] b & = \frac 3 \end \\ $$
Answer: $$b = \frac 3$$
Evaluate $$\displaystyle \lim_ f(x)$$ when $$f$$ is defined as follows.